Advertisements
Advertisements
प्रश्न
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
उत्तर
Let CD be the height of the aeroplane above the river at some instant. Suppose A and B be two points on both banks of the river in opposite directions
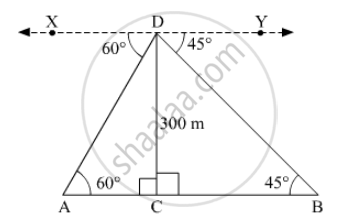
Height of the aeroplane above the river, CD = 300 m
Now,
∠CAD = ∠ADX = 60º (Alternate angles)
∠CBD = ∠BDY = 45º (Alternate angles)
In right ∆ACD,
`tan 60^@ = (CD)/(AC)`
`=> sqrt3 = 300/(AC)`
`=> AC = 300/sqrt3 = 100sqrt3 m`
In right ∆BCD
`tan 45^@ = (CD)/(BC)`
`=> 1 = 300/(BC)`
=> BC = 300 m
∴ Width of the river, AB
= BC + AC
`= 300 + 100sqrt3`
`= 300 + 100 xx 1.73`
= 300 + 173
= 473 m
Thus, the width of the river is 473 m
APPEARS IN
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
A tree breaks due to the storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 10 metres. Find the height of the tree.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
As observed form the top of a lighthouse, 100m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° and 60° . Determine the distance travelled by the ship during the period of observation.
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
