Advertisements
Advertisements
प्रश्न
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
विकल्प
\[3\sqrt{2}x\]
\[2\sqrt{3}x\]
\[\frac{\sqrt{3}}{2}x\]
\[\frac{2}{\sqrt{3}}x\]
उत्तर
Let h be the height of chimney AB

Given that: angle of elevation changes from angle `∠D=30°`to .`∠C=60°`
Then Distance becomes `CD=x` and we assume `BC=y`
Here, we have to find the height of chimeny.
So we use trigonometric ratios.
In a triangle,ABC
`⇒ tan C=(AB)/(BC)`
`⇒ tan 60°=(AB)/(BC)`
`⇒ sqrt3=h/y`
`⇒y=h/sqrt3`
Again in a triangle ABD,
`⇒ tan D=(AB)/(BC+CD)`
`⇒ tan 30°=h/(y+x)`
`⇒1/sqrt3=h/(y+x)`
`⇒sqrt3h=y+x`
`⇒sqrt3h=h/sqrt3+x` `["put" y=h/sqrt3]`
`⇒ h(sqrt3-1/sqrt3)=x`
`⇒h=x/(sqrt3-1/sqrt3)`
`⇒h=(sqrt3x)/2`
APPEARS IN
संबंधित प्रश्न
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
|
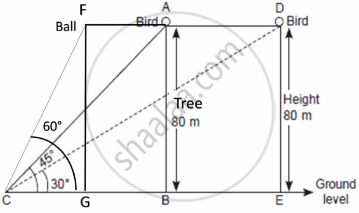
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?