Advertisements
Advertisements
प्रश्न
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
विकल्प
\[\left( \sqrt{3} + 1 \right) x\]
\[\left( \sqrt{3} - 1 \right) x\]
\[2\sqrt{3}x\]
\[3\sqrt{2}x\]
उत्तर
Let h be the height of tower AB
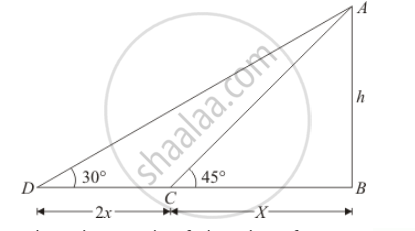
Given that: angle of elevation of sun are`∠D=30°` and.`∠C=45°`
Then Distance`CD=2x` and we assume `BC=x`Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=(AB)/(BC)`
`⇒ tan 45°=(AB)/(BC)`
`⇒ 1=h/x`
`⇒ x=h`
Again in a triangle ABD,
`⇒ tan D= (AB)/(BC+CD)`
`⇒ tan 30°=h/( x+2x)`
`⇒1/sqrt3=h/(h+2x)` `[x=h]`
`⇒ sqrt3h=h+2x`
`h(sqrt3-1)=2x`
`⇒ h=2x/(sqrt3-1)`
⇒` h=(2x)/(sqrt3-1)xx(sqrt3+1)/(sqrt3+1)`
`⇒ h=x(sqrt3+1)`
APPEARS IN
संबंधित प्रश्न
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The angle of elevation of a cloud from a point 60 m above the surface of the water of a lake is 30° and the angle of depression of its shadow in water of lake is 60°. Find the height of the cloud from the surface of water
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
A tower stands vertically on the ground. From a point on the ground which is 20 m away from the foot of the tower, the angle of elevation of its top is found to be 60°. Find the height of the tower. [Take `sqrt(3)` =1.732 ]
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
