Advertisements
Advertisements
प्रश्न
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
उत्तर
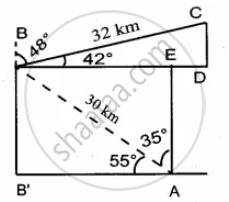
The distance of C to the East of B is BD
In the right ∆BDC,
cos 42° = `"BD"/"BC"`
0.7431 = `"BD"/32`
∴ BD = 0.7431 × 32
= 23.78 km
Distance of C to the East of B is 23.78 km.
APPEARS IN
संबंधित प्रश्न
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
