Advertisements
Advertisements
प्रश्न
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
उत्तर
Let A and B the position of the first ship and the second ship
Distance = `200((sqrt(3) + 1)/sqrt(3))`m
Let the height of the lighthouse CD be h
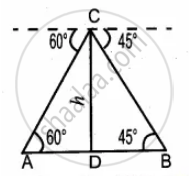
In the right ∆ACD, tan 60° = `"CD"/"AD"`
`sqrt(3) = "h"/"AD"`
∴ AD = `"h"/sqrt(3` ...(1)
In the right ∆BCD
tan 45° = `"DC"/"BD"`
1 = `"h"/"BD"`
∴ BD = h
Distance between the two ships = AD + BD
`200((sqrt(3) + 1)/sqrt3) = "h"/sqrt3 + "h"`
⇒ `200 (sqrt(3) + 1) = "h" + sqrt(3)"h"`
`200(sqrt(3) + 1) = "h"(1 + sqrt(3))`
⇒ h = `(200(sqrt(3) + 1))/((1 + sqrt(3))`
h = 200
Height of the light house = 200 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
From the top of a building 30 m high, the top and bottom of a tower are observed to have angles of depression 30º and 45º respectively. Find the height of the tower
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
A straight highway leads to the foot of a tower. A man standing on the top of the 75 m high tower observes two cars at angles of depression of 30° and 60°, which are approaching the foot of the tower. If one car is exactly behind the other on the same side of the tower, find the distance between the two cars. (use `sqrt(3)` = 1.73)
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
