Advertisements
Advertisements
प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
उत्तर
Let BC be the height at which the aeroplane is observed from point A.
Then, BC = 1500√3
In 15 seconds, the aeroplane moves from point A to D.
A and D are the points where the angles of elevation 60 and 30
are formed respectively.
Let BA = x metres and AD y metres
BC = x + y
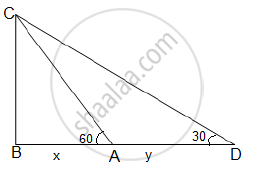
In ΔCBA,
`tan60^@="BC"/"BA"`
`sqrt3=(1500sqrt3)/x`
x=1500 m........(1)
In ΔCBD,
`tan30^@="BC"/"BD"`
`1/sqrt3=(1500sqrt3)/(x+y)`
x + y =1500(3)= 4500
1500 + y = 4500
y = 3000 m ....(2)
We know that the aeroplane moves from point A to D in 15 seconds and the distance covered is 3000 metres. (by 2)
`"speed"="distance"/"time"`
`"speed"=3000/15`
speed=200 m/s
Converting it to km/hr =200x(18/5)=720 km/hr
APPEARS IN
संबंधित प्रश्न
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
|
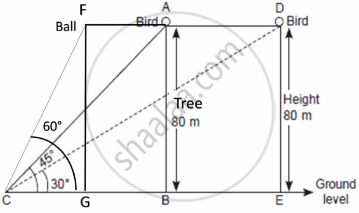
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)