Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
उत्तर
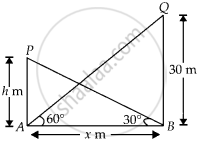
Let distance between the two towers = AB = x m
And height of the other tower = PA = h m
Given, height of the tower = QB = 30 m, ∠QAB = 60° and ∠PBA = 30°
Now, in ∆QAB,
tan 60° = `"QB"/"AB" = 30/x`
⇒ `sqrt(3) = 30/x`
⇒ `x = 30/sqrt(3)`
⇒ `x = 30/sqrt(3) * sqrt(3)/sqrt(3)`
= `(30sqrt(3))/3`
= `10sqrt(3)`
And in ∆PBA,
tan 30° = `"PA"/"AB" = "h"/x`
⇒ `1/sqrt(3) = "h"/(10sqrt(3))` ...`[∵ x = 10sqrt(3) "m"]`
⇒ h = 10
Hence, the required distance and height are `10sqrt(3) "m"` and 10 m, respectively.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
