Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
उत्तर
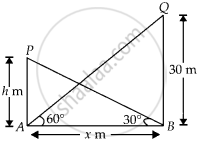
Let distance between the two towers = AB = x m
And height of the other tower = PA = h m
Given, height of the tower = QB = 30 m, ∠QAB = 60° and ∠PBA = 30°
Now, in ∆QAB,
tan 60° = `"QB"/"AB" = 30/x`
⇒ `sqrt(3) = 30/x`
⇒ `x = 30/sqrt(3)`
⇒ `x = 30/sqrt(3) * sqrt(3)/sqrt(3)`
= `(30sqrt(3))/3`
= `10sqrt(3)`
And in ∆PBA,
tan 30° = `"PA"/"AB" = "h"/x`
⇒ `1/sqrt(3) = "h"/(10sqrt(3))` ...`[∵ x = 10sqrt(3) "m"]`
⇒ h = 10
Hence, the required distance and height are `10sqrt(3) "m"` and 10 m, respectively.
APPEARS IN
संबंधित प्रश्न
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is:
(A) `4/sqrt3`
(B) `4sqrt3`
(C) `2sqrt2`
(D)4
The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them.
If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
