Advertisements
Advertisements
Question
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
Solution
Let BC be the height at which the aeroplane is observed from point A.
Then, BC = 1500√3
In 15 seconds, the aeroplane moves from point A to D.
A and D are the points where the angles of elevation 60 and 30
are formed respectively.
Let BA = x metres and AD y metres
BC = x + y
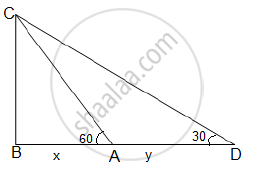
In ΔCBA,
`tan60^@="BC"/"BA"`
`sqrt3=(1500sqrt3)/x`
x=1500 m........(1)
In ΔCBD,
`tan30^@="BC"/"BD"`
`1/sqrt3=(1500sqrt3)/(x+y)`
x + y =1500(3)= 4500
1500 + y = 4500
y = 3000 m ....(2)
We know that the aeroplane moves from point A to D in 15 seconds and the distance covered is 3000 metres. (by 2)
`"speed"="distance"/"time"`
`"speed"=3000/15`
speed=200 m/s
Converting it to km/hr =200x(18/5)=720 km/hr
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A tree standing on a horizontal plane is leaning towards the east. At two points situated at distances a and b exactly due west on it, the angles of elevation of the top are respectively α and β. Prove that the height of the top from the ground is `((b - a)tan alpha tan beta)/(tan alpha - tan beta)`
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
