Advertisements
Advertisements
Question
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
Solution
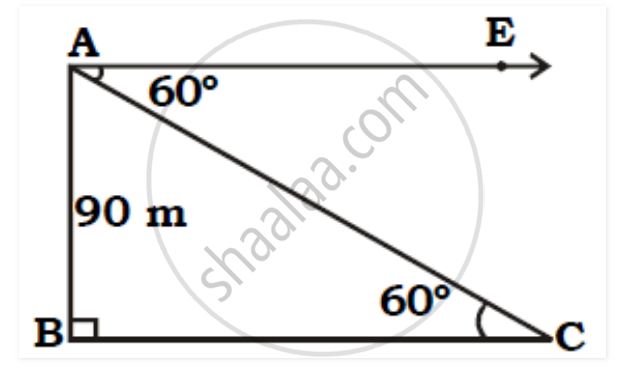
As shown in the figure, assume AB as the lighthouse and let A be the position of the observer and C be the position of the ship. Let the distance from the ship to the lighthouse be x.
Let AB be the height of the lighthouse,
∴ AB = 84 metres [Given]
The point 'C' be the position of the ship,
∴ ∠ ACB = 60°
`tan 60° = ("Opposite side of "60°) /("Adjacent side of "60°)`
∴ `tan 60° = "AB" / "BC"`
∴ `sqrt3 = 84/"BC"`
∴ `"BC" = 84/sqrt3`
∴ `"BC" = (84/sqrt3)×sqrt3/sqrt3`
∴ BC = 28√3
∴ BC = 28× 1.73
∴ BC = 48.4 m.
∴ The ship is 48.4 m away from the lighthouse.
APPEARS IN
RELATED QUESTIONS
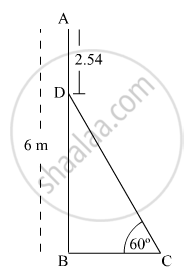
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
From the top of a tower of height 50 m, the angles of depression of the top and bottom of a pole are 30° and 45° respectively. Find
(i) how far the pole is from the bottom of a tower,
(ii) the height of the pole. (Use \[\sqrt{3} = 1 . 732\])
A solid right circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is
Two buildings are in front of each other on a road of width 15 meters. From the top of the first building, having a height of 12 meter, the angle of elevation of the top of the second building is 30°.What is the height of the second building?

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
An observer , 1.7 m tall , is` 20 sqrt3` m away from a tower . The angle of elevation from the eye of an observer to the top of tower is 300 . Find the height of the tower.
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
A window of a house is h meters above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be A and B respectively. Then the height of the other house is ____________.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°. Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If ∠BAQ = 30°, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is ______.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
