Advertisements
Advertisements
Question
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
Solution
Let the height of the tower be h m.
Given, tan α = `1/3` and tan β = `3/4`
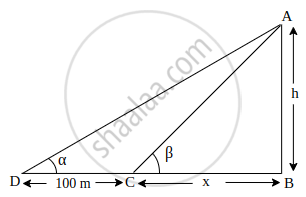
Now, In ΔABD, ∠D = α, ∠B = 90°
tan α = `("AB")/("DB")`
⇒ `1/3 = "h"/(100 + x)`
⇒ 100 + x = 3h
⇒ x = 3h – 100 ...(i)
In ΔABC, ∠C = β, ∠B = 90°
tan β = `("AB")/("BC")`
⇒ `3/4 = "h"/x`
⇒ x = `(4"h")/3` ...(ii)
From equations (i) and (ii), we have
3h – 100 = `(4"h")/3`
⇒ `3"h" - (4"h")/3` = 100
⇒ `(5"h")/3` = 100
⇒ h = `300/5`
⇒ h = 60 m
Hence, the height of the tower is 60 m.
APPEARS IN
RELATED QUESTIONS
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 2.5m from the banks, find the width of the river.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
The Distance of the point (−3, 4) from the x-axis is
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
Find the length of the shadow on the ground of a pole of height 18m when angle of elevation θ of the sun is such that tan θ = `6/7`.
