Advertisements
Advertisements
प्रश्न
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
उत्तर
Let the height of the tower be h m.
Given, tan α = `1/3` and tan β = `3/4`
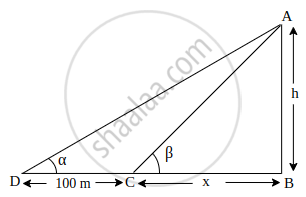
Now, In ΔABD, ∠D = α, ∠B = 90°
tan α = `("AB")/("DB")`
⇒ `1/3 = "h"/(100 + x)`
⇒ 100 + x = 3h
⇒ x = 3h – 100 ...(i)
In ΔABC, ∠C = β, ∠B = 90°
tan β = `("AB")/("BC")`
⇒ `3/4 = "h"/x`
⇒ x = `(4"h")/3` ...(ii)
From equations (i) and (ii), we have
3h – 100 = `(4"h")/3`
⇒ `3"h" - (4"h")/3` = 100
⇒ `(5"h")/3` = 100
⇒ h = `300/5`
⇒ h = 60 m
Hence, the height of the tower is 60 m.
APPEARS IN
संबंधित प्रश्न
Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
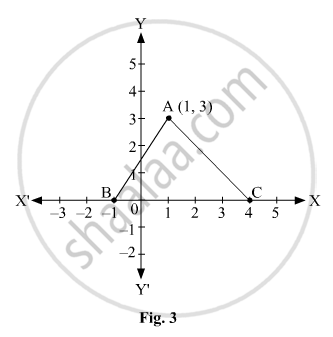
In Fig. 3, the area of triangle ABC (in sq. units) is:
A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is
60°. Find the length of the string assuming that there is no slack in the string.
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
In figure given ABCD is a rectangle, the value of CE is ____________.

A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
