Advertisements
Advertisements
प्रश्न
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
उत्तर
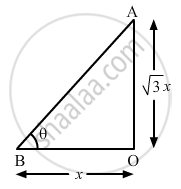
Let AO be the pole and OB be its shadow.
Let the length of the shadow be x.
Let θ be the angle of elevation of the Sun at that time.
Given:
Height of pole (h) =\[\sqrt{3} \times\] Length of its shadow
We have:
\[\tan \theta = \frac{AO}{OB}\]
\[ = \frac{h}{x}\]
\[ = \frac{\sqrt{3}x}{x}\]
\[ = \sqrt{3}\]
\[ \Rightarrow \tan \theta = \tan 60^o\]
\[ \Rightarrow \theta = {60}^\circ\]
Thus, the angle of elevation of the Sun is 60°.
Hence, the correct option is B.
APPEARS IN
संबंधित प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
