Advertisements
Advertisements
प्रश्न
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
विकल्प
\[\frac{h}{2} m\]
\[\sqrt{3h} m\]
\[\frac{h}{3} m\]
\[\frac{h}{\sqrt{3}}m\]
उत्तर
Let AB be the tower and C is a point on the same level as its foot such that ∠ACB = 30°
The given situation can be represented as,
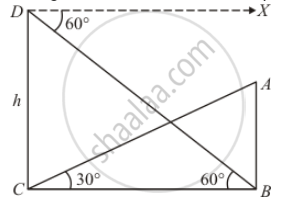
Here D is a point h m above the point C.
In ΔBCD,
`⇒ tan B=(CD)/(CB)`
`⇒ tan 60°=h/(CB)`
`⇒ sqrt3=h/(CB)`
`⇒ CB=h/sqrt3`
Again in triangle ABC,
`tan C=(AB)/(CB)`
`⇒ tan30= (AB)/((h/sqrt3))` [Using (1)]
`⇒1/sqrt3=AB/((h/sqrt3))`
`⇒ AB=h/3`
APPEARS IN
संबंधित प्रश्न
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the East of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
Read the following passage:
|
Radio towers are used for transmitting a range of communication services including radio and television. The tower will either act as an antenna itself or support one or more antennas on its structure; On a similar concept, a radio station tower was built in two Sections A and B. Tower is supported by wires from a point O. Distance between the base of the tower and point O is 36 cm. From point O, the angle of elevation of the top of the Section B is 30° and the angle of elevation of the top of Section A is 45°.
|
Based on the above information, answer the following questions:
- Find the length of the wire from the point O to the top of Section B.
- Find the distance AB.
OR
Find the area of ∠OPB. - Find the height of the Section A from the base of the tower.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)

