Advertisements
Advertisements
प्रश्न
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
विकल्प
h tan (45° + θ)
h cot (45° − θ)
h tan (45° − θ)
h cot (45° + θ)
उत्तर
Let AB be the surface of the lake and p be the point of observation. So AP=h . The given situation can be represented as,
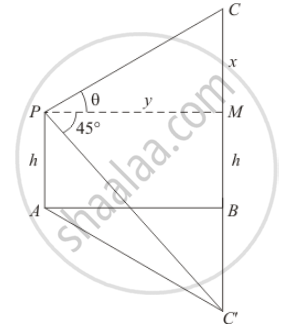
Here,C is the position of the cloud and C' is the reflection in the lake. Then .`CB=C'B`
Let PM be the perpendicular from P on CB. Then `∠CPM=θ` and .`∠C'PM=45°`
Let`CM=x` , `PM=y` , then`CB=x+h` and `C'B=x+h`
Here, we have to find the height of cloud.
So we use trigonometric ratios.
In , `ΔCMP`
`⇒ tan θ=(CM)/(PM)`
`⇒ tanθ=x/y`
`⇒ y= x/tanθ ` (1)
Again in ΔPMC',
`⇒ tan 45°=CM/PM`
`⇒1=(C'B+BM)/(PM)`
`⇒1=(x+h+h)/y`
`⇒y=x+2h`
`⇒ x/tanθ=x+2h` [using (1)]
`⇒ (x-x tanθ)/tan θ=2h`
`⇒ x=(2h tan θ)/((1-tan θ))`
Now,
`⇒ CB=h+x`
`⇒ CB=h+(2h tan θ)/(1-tan θ)`
`⇒ CB=(h(1-tanθ)+2h tanθ)/(1-tan θ)`
`⇒ CB= (h(1+tan θ))/(1-tan θ)=h tan(45°+ θ )` `[tan (A+B)=(tan A+tan B)/(1-tan A tan B)] `
APPEARS IN
संबंधित प्रश्न
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 2.5m from the banks, find the width of the river.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
If the altitude of the sum is at 60°, then the height of the vertical tower that will cast a shadow of length 30 m is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
