Advertisements
Advertisements
प्रश्न
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

उत्तर १
In ΔABC,
`("AB")/("BC")` = tan 60°
`("AB")/("BC") = sqrt3`
`"BC" = ("AB")/sqrt3`
In ΔABD,
`("AB")/("BD") `= tan 30°
`("AB")/("BC"+"CD") = 1/sqrt3`
`("AB")/(("AB")/sqrt3+20) = 1/sqrt3`
`("AB"sqrt3)/("AB"+20sqrt3) = 1/sqrt3`
`3"AB" = "AB"+20sqrt3`
`2"AB" = 20sqrt3`
`"AB" = 10sqrt3 m`
`"BC" = ("AB")/sqrt3`
= `((10sqrt3)/sqrt3)m`
= 10 m
Therefore, the height of the tower is `10sqrt3` m and the width of the canal is 10 m.
उत्तर २
Let PQ = h m be the height of the TV tower and BQ = x m be the width of the canal.
We have,
AB = 20 m, ∠PAQ = 30°, ∠BQ = x and PQ = h
In ΔPBQ,
`tan 60° = ("PQ")/("BQ")`
⇒ `sqrt(3) = h/x`
⇒ `h = x sqrt(3) ` ...(1)
Again in ΔAPQ,
`tan 30° = ("PQ")/("AQ")`
⇒ `1/sqrt(3) = h/("AB" +"BQ")`
⇒ `1/sqrt(3) = (x sqrt(3))/(20+3)` ...[Using (1)]
⇒ 3x = 20 + x
⇒ 3x - x = 20
⇒ 2x = 20
⇒ x = `20/2`
⇒ x = 10 m
Substituting x = 10 in (i), we get
h = `10 sqrt(3)` m
So, the height of the TV tower is 10`sqrt(3)` m and the width of the canal is 10 m.
संबंधित प्रश्न
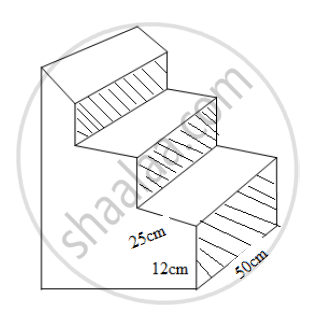
There are three stair-steps as shown in the figure below. Each stair step has width 25 cm, height 12 cm and length 50 cm. How many bricks have been used in it, if each brick is 12.5 cm x 6.25 cm x 4 cm?
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
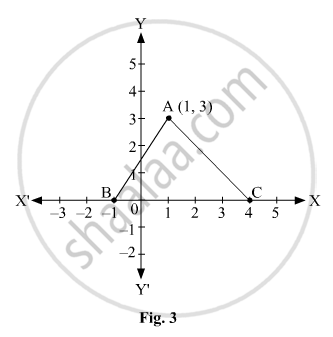
In Fig. 3, the area of triangle ABC (in sq. units) is:
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
Three villagers A, B and C can see each other using telescope across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate the vertical height between B and C. (tan 20° = 0.3640, `sqrt3` = 1.732)

A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
Read the following passage and answer the questions given below.
|
Kite Festival Kite festival is celebrated in many countries at different times of the year. In India, every year 14th January is celebrated as International Kite Day. On this day many people visit India and participate in the festival by flying various kinds of kites. The picture given below, show three kites flying together.
In the given figure, the angles of elevation of two kites (Points A and B) from the hands of a man (Point C) are found to be 30° and 60° respectively. Taking AD = 50 m and BE = 60 m, find. |
- the lengths of strings used (take them straight) for kites A and B as shown in the figure.
- the distance 'd' between these two kites.
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.


