Advertisements
Advertisements
प्रश्न
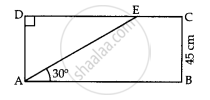
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

उत्तर १
In ΔABC,
`("AB")/("BC")` = tan 60°
`("AB")/("BC") = sqrt3`
`"BC" = ("AB")/sqrt3`
In ΔABD,
`("AB")/("BD") `= tan 30°
`("AB")/("BC"+"CD") = 1/sqrt3`
`("AB")/(("AB")/sqrt3+20) = 1/sqrt3`
`("AB"sqrt3)/("AB"+20sqrt3) = 1/sqrt3`
`3"AB" = "AB"+20sqrt3`
`2"AB" = 20sqrt3`
`"AB" = 10sqrt3 m`
`"BC" = ("AB")/sqrt3`
= `((10sqrt3)/sqrt3)m`
= 10 m
Therefore, the height of the tower is `10sqrt3` m and the width of the canal is 10 m.
उत्तर २
Let PQ = h m be the height of the TV tower and BQ = x m be the width of the canal.
We have,
AB = 20 m, ∠PAQ = 30°, ∠BQ = x and PQ = h
In ΔPBQ,
`tan 60° = ("PQ")/("BQ")`
⇒ `sqrt(3) = h/x`
⇒ `h = x sqrt(3) ` ...(1)
Again in ΔAPQ,
`tan 30° = ("PQ")/("AQ")`
⇒ `1/sqrt(3) = h/("AB" +"BQ")`
⇒ `1/sqrt(3) = (x sqrt(3))/(20+3)` ...[Using (1)]
⇒ 3x = 20 + x
⇒ 3x - x = 20
⇒ 2x = 20
⇒ x = `20/2`
⇒ x = 10 m
Substituting x = 10 in (i), we get
h = `10 sqrt(3)` m
So, the height of the TV tower is 10`sqrt(3)` m and the width of the canal is 10 m.
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
Two poles of equal heights are standing opposite to each other on either side of the road which is 80m wide, From a point P between them on the road, the angle of elevation of the top of one pole is 60 and the angle of depression from the top of another pole at P is 30 . Find the height of each pole and distance of the point P from the poles.
The lower window of a house is at a height of 2 m above the ground and its upper window is 4 m vertically above the lower window. At certain instant the angles of elevation of a balloon from these windows are observed to be 60° and 30° respectively. Find the height of the balloon above the ground.
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
In given figure, the value of AE is ____________.
In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan `theta` is ____________.

The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
Lakshaman Jhula is located 5 kilometers north-east of the city of Rishikesh in the Indian state of Uttarakhand. The bridge connects the villages of Tapovan to Jonk. Tapovan is in Tehri Garhwal district, on the west bank of the river, while Jonk is in Pauri Garhwal district, on the east bank. Lakshman Jhula is a pedestrian bridge also used by motorbikes. It is a landmark of Rishikesh. A group of Class X students visited Rishikesh in Uttarakhand on a trip. They observed from a point (P) on a river bridge that the angles of depression of opposite banks of the river are 60° and 30° respectively. The height of the bridge is about 18 meters from the river. |
Based on the above information answer the following questions.
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river.
[OR]
Find the height BQ if the angle of the elevation from P to Q be 30°.
