Advertisements
Advertisements
प्रश्न
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
उत्तर
Let OX be the horizontal plane, AD be the tower and CD be the vertical flagpole
We have:
AB = 9m, ∠DBA= 30° and ∠CBA = 60°
Let:
AD = hm and CD = xm
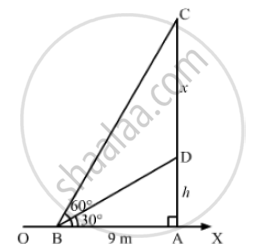
In the right ΔABD,we have:
`(AD)/(AB) = tan 30° = 1/ sqrt(3)`
`⇒ h/8 = 1/sqrt(3)`
`⇒ h = 9/sqrt(3) = 5.19 `m
Now, in the right ΔABC,we have
`(AC)/(BA) = tan 60° = sqrt(3)`
`⇒ (h+x ) /9 = sqrt(3)`
`⇒ h + x = 9 sqrt(3)`
By putting h= `9/sqrt(3)` in the above equation, we get:
`9/sqrt(3) + x = 9 sqrt(3) `
`⇒ x = 9 sqrt(3) - 9/ sqrt(3) `
`⇒ x = (27-9)/ sqrt(3) = 18/ sqrt(3) = 18/ 1.73 = 10.4`
Thus, we have:
Height of the flagpole = 10. 4 m
Height of the tower = 5. 19 m
APPEARS IN
संबंधित प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
If a tower 30 m high, casts a shadow `10sqrt3` m long on the ground, then what is the angle of elevation of the sun?
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
A boy standing at a distance of 48 meters from a building observes the top of the building and makes an angle of elevation of 30°. Find the height of the building.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
From the top of a tower h m high, the angles of depression of two objects, which are in line with the foot of the tower are α and β (β > α). Find the distance between the two objects.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
