Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
उत्तर
Let AB be the unfinished tower, AC be the raised tower and O be the point of observation
We have:
OA = 75m,∠AOB = 30° and ∠AOC = 60°
Let AC = H m such that BC = (H -h)m.
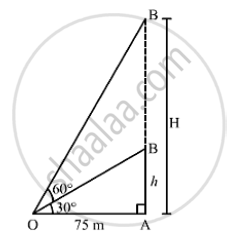
In ΔAOB,we have:
`(AB)/(OA) = tan 30° = 1/ sqrt(3)`
`⇒ h/ 75 = 1/ sqrt(3)`
`⇒ = 75/ sqrt(3) m = (75 xx sqrt(3)) /(sqrt(3) xx sqrt(3)) = 25 sqrt(3) m`
In ΔAOC,we have:
`(AC)/(OA) = tan 60° = sqrt(3)`
`⇒ H/75 = sqrt(3)`
`⇒ H = 75 sqrt(3 )m`
`∴"Required height" =(H - h) = (75 sqrt(3) - 25 sqrt(3)) = 50 sqrt(3)m = 86.6m`
APPEARS IN
संबंधित प्रश्न
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building (use `sqrt3`=1.73)
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
The angles of depression of the top and bottom of 8 m tall building from the top of a multistoried building are 30° and 45° respectively. Find the height of the multistoried building and the distance between the two buildings.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of tower. Then the height of tower is ______.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
