Advertisements
Advertisements
प्रश्न
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
उत्तर
Let h be the height of tower AB and angle of elevation are 45° and 60° are given.
In a triangle OAC, given that AB = 10+x and BC = x
Now we have to find the height of the tower.
So we use trigonometrical ratios.
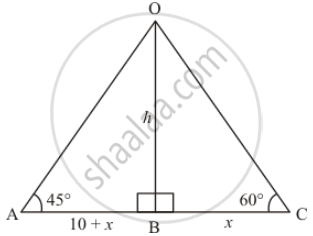
In a triangle OAB,
`=> tan A = (OB)/(AB)`
`=> tan 45^@ = (OB)/(AB)`
`=> 1= h/(10 + x)`
=> h = 10 + x
Therefore x = h - 10
Again in a triangle OCB
`=> tan C = (OB)/(BC)`
`=> tan 60^@ = (OB)/(BC)`
`=> sqrt3 = h/x`
`=> h = sqrt3x`
Put x = h - 10
`=> h = sqrt3 (h - 10)`
`=> h = sqrt3h - 10sqrt3`
`=> 10sqrt3 = h(sqrt3 - 1)`
`=> h = (10sqrt3)/(sqrt3 - 1)`
`=> h = (10 xx 1.732)/(1.732 - 1)`
`=> h = 17.32/0.327`
=> h = 23.66
Hence height of tower is 23.66 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of tower is 45. Find the height of the tower PQ and the distance PX. (Use `sqrt3=1.73)`
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
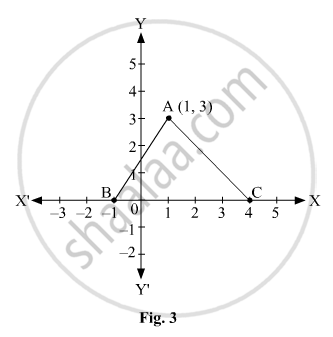
In Fig. 3, the area of triangle ABC (in sq. units) is:
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
