Advertisements
Advertisements
प्रश्न
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
उत्तर
Let AB be the tower of height h. And person makes an angle of elevation of the top of a tower is 30°, he walks 50 m towards the foot of tower then makes an angle of elevation of 60°
Let BC = x, CD = 50, and ∠ACB = 60°, ∠ADB = 30°
Now we have to find the height of the tower.
We have the corresponding figure as follows
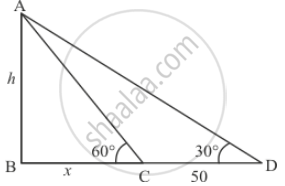
So we use trigonometric ratios.
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60^@ = h/x`
`=> sqrt3 = h/x`
`=> x = h/sqrt3`
Again in a triangle ADB,
`=> tan D = (AB)/(BC + CD)`
`=> tan 30^@ = h/(x + 50)`
`=> 1/sqrt3 = h/(x + 50)`
`=> sqrt3h = x + 50`
`=> 3h = h + 50sqrt3`
`=> 2h = 50sqrt3`
`=> h = 25sqrt3`
=> h = 25 x 1.73
=> h = 43.25
Hence the height of tower is 43.25 m
APPEARS IN
संबंधित प्रश्न
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building (use `sqrt3`=1.73)
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
From the top of a hill, the angles of depression of two consecutive kilometer stones due east are found to be 45° and 30° respectivly. Find the height of the hill ?
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
A pole of height 30 m is observed from a point. The angle of depression of the point is 30°. Find the distance of the point from the base of the pole.
