Advertisements
Advertisements
प्रश्न
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
पर्याय
`20, 10sqrt(3)`
`30, 5sqrt(3)`
20, 10
`30, 10sqrt(3)`
उत्तर
`30, 10sqrt(3)`
Explanation;
Hint:
Let the height of the multistoried building AB be h
AE = h – 20
Let BC be x
In the right ∆ABC, tan 60° = `"AB"/"BC"`
⇒ `sqrt(3) = "h"/x`
x = `"h"/sqrt(3)` ...(1)
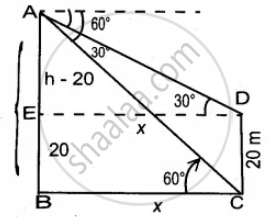
In the right ∆ABC, tan 30° = `"AE"/"ED" = ("h" - 20)/x`
`1/sqrt(3) = ("h" - 20)/x`
`1/sqrt(3) = ("h" - 20)/x`
x = `("h" - 20) sqrt(3)` ...(2)
From (1) and (2) we get,
`"h"/sqrt(3) = ("h" - 20) sqrt(3)`
h = 3h – 60
⇒ 60 = 2h
h = `60/2` = 30
Distance between the building (x) =
`"h"/sqrt(3) = 30/sqrt(3)`
= `(30sqrt(3))/3`
= `10sqrt(3)`
APPEARS IN
संबंधित प्रश्न
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
An observed from the top of a 150 m tall lighthouse, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the West of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
