Advertisements
Advertisements
Question
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
Options
`20, 10sqrt(3)`
`30, 5sqrt(3)`
20, 10
`30, 10sqrt(3)`
Solution
`30, 10sqrt(3)`
Explanation;
Hint:
Let the height of the multistoried building AB be h
AE = h – 20
Let BC be x
In the right ∆ABC, tan 60° = `"AB"/"BC"`
⇒ `sqrt(3) = "h"/x`
x = `"h"/sqrt(3)` ...(1)
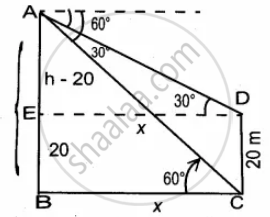
In the right ∆ABC, tan 30° = `"AE"/"ED" = ("h" - 20)/x`
`1/sqrt(3) = ("h" - 20)/x`
`1/sqrt(3) = ("h" - 20)/x`
x = `("h" - 20) sqrt(3)` ...(2)
From (1) and (2) we get,
`"h"/sqrt(3) = ("h" - 20) sqrt(3)`
h = 3h – 60
⇒ 60 = 2h
h = `60/2` = 30
Distance between the building (x) =
`"h"/sqrt(3) = 30/sqrt(3)`
= `(30sqrt(3))/3`
= `10sqrt(3)`
APPEARS IN
RELATED QUESTIONS
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 90 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
A tree is broken by the wind. The top of that tree struck the ground at an angle of 30° and at a distance of 30. Find the height of the whole tree
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
The angle of elevation of an aeroplane from a point on the ground is 45° after flying for 15seconds, the elevation changes to 30° . If the aeroplane is flying at a height of 2500 meters, find the speed of the areoplane.
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.
At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the distance travelled by the plane in 30 seconds?
OR
Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration. - What is the speed of the plane in km/hr.
