Question

A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`

Answer 1

Let PQ be the ladder such that its top Q is on the wall OQ  and bottom P is on the ground. The ladder is pulled away from the wall through a distance a, so that its top Q slides and takes position Q'. So PQ = P'Q'

∠QPQ = α And ∠QP'Q' = β.

Let PQ = h

We have to prove that

`a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`

We have the corresponding figure as follows

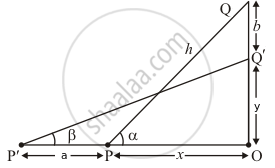
In ΔPOQ

`=> sin alpha = (OQ)/(PQ)`

`=> sin alpha = (b + y)/h`

And

`=> cos alpha = (OP)/(PQ)`

`=> cos alpha = x/h`

Again in ΔP'OQ'

`=> sin beta = (OQ')/(P'Q')`

`=> sin beta = y/h`

And

`=> cos beta = (OP')/(P'Q')`

`=> cos beta = (a + x)/h`

Now

`=> sin alpha - sin beta = (b + y)/h - y/h`

`=> sin alpha - sin beta = b/h`

And

`=> cos beta  - cos alpha = (a + x)/h = x/h`

`=> cos beta - cos alpha = a/h`

So

`=> (sin alpha - sin beta)/(cos beta - cos alpha) = b/a`

`=> a/b = (sin beta cos alpha)/(sin beta - sin alpha)`

`=> a/b =  (cos alpha - cos beta)/(sin beta - sin alpha)`

Hence `a/b = (cos alpha  - cos beta)/(sin beta - sin alpha)`

Answer 2

Initial Position: Angle is α. The height on the wall is h₁ and the distance from the wall is x₁.

Final Position: Angle is β. The height on the wall is h₂ and the distance from the wall is x₂.

x₁ = L cos α and h₁ = L sin α

x₂ = L cos β and h₂ = L sin β

The foot is pulled away by distance a: a = x₂ – x₁

The top slides down by distance b: b = h₁ – h₂

a = L cos β - L cos α = L cos α

= L(cos β - cos α)

b = L sin α - L sin β 

= L(sin α - sin β)

alculate the Ratio `a/b`

`a/b = (L(cosbeta - cosalpha))/(L (sinalpha - sinbeta))`

`a/b = (-(cosbeta - cosalpha))/-(sinalpha - sinbeta)`

`a/b = (cosalpha - cos beta)/(sin beta - sin alpha)`