Question

A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`

 

Answer 1

Let PQ be the ladder such that its top Q is on the wall OQ  and bottom P is on the ground. The ladder is pulled away from the wall through a distance a, so that its top Q slides and takes position Q'. So PQ = P'Q'

∠QPQ = α And ∠QP'Q' = β.

Let PQ = h

We have to prove that

`a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`

We have the corresponding figure as follows

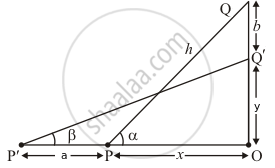
In ΔPOQ

`=> sin alpha = (OQ)/(PQ)`

`=> sin alpha = (b + y)/h`

And

`=> cos alpha = (OP)/(PQ)`

`=> cos alpha = x/h`

Again in ΔP'OQ'

`=> sin beta = (OQ')/(P'Q')`

`=> sin beta = y/h`

And

`=> cos beta = (OP')/(P'Q')`

`=> cos beta = (a + x)/h`

Now

`=> sin alpha - sin beta = (b + y)/h - y/h`

`=> sin alpha - sin beta = b/h`

And

`=> cos beta  - cos alpha = (a + x)/h = x/h`

`=> cos beta - cos alpha = a/h`

So

`=> (sin alpha - sin beta)/(cos beta - cos alpha) = b/a`

`=> a/b = (so beta 0 cos alpha)/(sin beta - sin alpha)`

`=> a/b =  (cos alpha - cos beta)/(sin beta - sin alpha)`

Hence `a/b = (cos alpha  - cos beta)/(sin beta - sin alpha)`