Question

The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is 

विकल्प

• `20, 10sqrt(3)`

• `30, 5sqrt(3)`

• 20, 10

• `30, 10sqrt(3)`

Answer 1

`30, 10sqrt(3)`

Explanation;

Hint:

Let the height of the multistoried building AB be h

AE = h – 20

Let BC be x

In the right ∆ABC, tan 60° = `"AB"/"BC"`

⇒ `sqrt(3) = "h"/x`

x = `"h"/sqrt(3)`  ...(1)

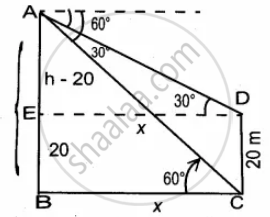
In the right ∆ABC, tan 30° = `"AE"/"ED" = ("h" - 20)/x`

`1/sqrt(3) = ("h" - 20)/x`

`1/sqrt(3) = ("h" - 20)/x`

x = `("h" - 20) sqrt(3)`  ...(2)

From (1) and (2) we get,

`"h"/sqrt(3) = ("h" - 20) sqrt(3)`

h = 3h – 60

⇒ 60 = 2h

h = `60/2` = 30

Distance between the building (x) =

`"h"/sqrt(3) = 30/sqrt(3)`

= `(30sqrt(3))/3`

= `10sqrt(3)`