Advertisements
Advertisements
प्रश्न
A person observed the angle of elevation of the top of a tower as 30°. He walked 50 m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60°. Find the height of the tower.
उत्तर
Let AB be the tower of height h. And person makes an angle of elevation of the top of a tower is 30°, he walks 50 m towards the foot of tower then makes an angle of elevation of 60°
Let BC = x, CD = 50, and ∠ACB = 60°, ∠ADB = 30°
Now we have to find the height of the tower.
We have the corresponding figure as follows
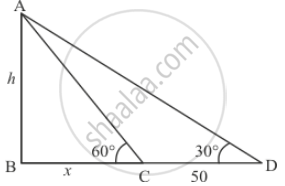
So we use trigonometric ratios.
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60^@ = h/x`
`=> sqrt3 = h/x`
`=> x = h/sqrt3`
Again in a triangle ADB,
`=> tan D = (AB)/(BC + CD)`
`=> tan 30^@ = h/(x + 50)`
`=> 1/sqrt3 = h/(x + 50)`
`=> sqrt3h = x + 50`
`=> 3h = h + 50sqrt3`
`=> 2h = 50sqrt3`
`=> h = 25sqrt3`
=> h = 25 x 1.73
=> h = 43.25
Hence the height of tower is 43.25 m
APPEARS IN
संबंधित प्रश्न
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
A TV tower stands vertically on a bank of a canal, with a height of `10 sqrt3` m. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the distance between the opposite bank of the canal and the point with a 30° angle of elevation.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
