Advertisements
Advertisements
प्रश्न
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
उत्तर
Let h be the height of the light house.
Let us suppose that the distance of one of the ships from the light house is x metres. Then, the distance of the other ship from the light house will be 100 − x metres.
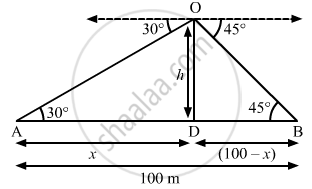
In right-angled triangle ADO, we have:
\[ \Rightarrow \frac{1}{\sqrt{3}} = \frac{h}{x}\]
\[ \Rightarrow x = \sqrt{3}h . . . (1)\]
\[ \Rightarrow 1 = \frac{h}{100 - x}\]
\[ \Rightarrow x + h = 100\]
\[\text{On putting x} = \sqrt{3}h, \text{we get}: \]
\[\sqrt{3}h + h = 100\]
\[ \Rightarrow h\left( \sqrt{3} + 1 \right) = 100\]
\[ \Rightarrow h = \frac{100}{\sqrt{3} + 1}\]
\[ \Rightarrow h = \frac{100}{\left( \sqrt{3} + 1 \right)} \times \frac{\left( \sqrt{3} - 1 \right)}{\left( \sqrt{3} - 1 \right)}\]
\[ \Rightarrow h = \frac{100}{2}\left( \sqrt{3} - 1 \right)\]
\[ \Rightarrow h = 36 . 6 (\text{approx} . )\]
APPEARS IN
संबंधित प्रश्न
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
From a point on a bridge across a river, the angles of depression of the banks on opposite side of the river are 30° and 45° respectively. If the bridge is at the height of 30 m from the banks, find the width of the river.
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.
At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the distance travelled by the plane in 30 seconds?
OR
Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration. - What is the speed of the plane in km/hr.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
