Advertisements
Advertisements
प्रश्न
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by a wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
उत्तर
Let AC and BD are the two poles with heights of 25 m and 35 m, respectively.
Draw a horizontal line from point C to the line BD, and it meets BD at E (say).
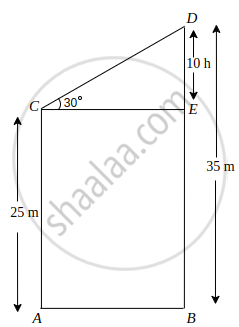
∴ DE = 35 – 25 = 10 m
In ΔCDE, tan 30° = `("DE")/("CE")`
⇒ `1/sqrt(3) = 10/("CE")`
⇒ CE = `10sqrt(3)` m
Thus, distance between the poles = BA = CE = `10sqrt(3)` m
Again, In ΔCDE, sin 30° = `("DE")/("CD")`
⇒ `1/2 = 10/("CD")`
⇒ CD = 20 m
Hence, length of the wire is 20 m.
संबंधित प्रश्न
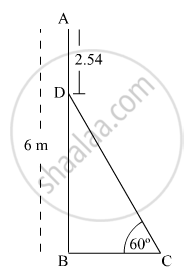
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
From the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45° and 60° respectively. Find the height of the pole.
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
