Advertisements
Advertisements
प्रश्न
As observed from the top of a 100 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. [Use `sqrt3` = 1.732]
उत्तर
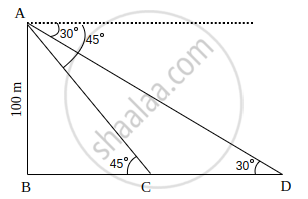
Let AB be the lighthouse and two ships be at point C and D.
In ΔABC,
tan 45° = `(AB)/(BC)`
⇒ 1 = `100/(BC)`
⇒ BC = 100 m
In ΔABD,
⇒ tan 30° = `(AB)/(BD)`
⇒ `1/sqrt(3) = 100/(100 + CD)`
⇒ 100 + CD = `100sqrt(3)`
⇒ CD = `100(sqrt(3) - 1)`
⇒ CD = 100(1.732 – 1)
⇒ CD = 100 × 0.732
⇒ CD = 73.2 m
Therefore, the distance between the two ships is 73.2 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60° and the angle of elevation of the top of the second tower from the foot of the first tower is 30°. Find the distance between the two towers and also the height of the other tower.
