Advertisements
Advertisements
प्रश्न
The angle of depression form the top of a tower of a point A on the ground is 30° . On moving a distance of 20 meters from the point A towards the foot of the tower to a point B, the angle of elevation of the top of the tower to from the point B is 60° . Find the height of the tower and its distance from the point A.
उत्तर
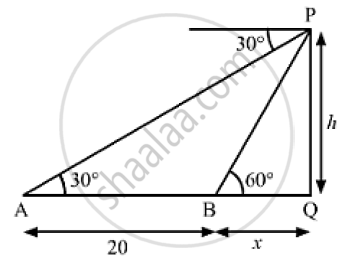
Let PQ be the tower.
We have,
AB = 20m, ∠PAQ = 30° and ∠PBQ = 60°
Let BQ = x and PQ = h
In ΔPBQ,
` tan 60° = (PQ)/(BQ) `
`⇒ sqrt(3) = h/x`
`⇒ = x sqrt(3) ` .......(1)
Also, in ΔAPQ ,
` tan 30° = (PQ)/(AQ)`
`⇒ 1/ sqrt(3) = h/(AB +BQ)`
`⇒ 1/ sqrt(3) = (x sqrt(3))/(20+x)` [Using (1)]
⇒ 20+ x = 3x
⇒ 3x -x = 20
⇒ 2x = 20
`⇒ =20/2`
⇒ x = 10 m
From (i),
`h = 10 sqrt(3)=10xx1.732 =17.32m`
Also, AQ = AB+BQ = 20 + 10 = 30m
So, the height of the tower is 17. 32 m and its distance from the point A is 30 m.
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
Find the angle of elevation of the sum (sun's altitude) when the length of the shadow of a vertical pole is equal to its height.
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
Find the distance between the points (a, b) and (−a, −b).
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take `sqrt(3)` = 1.73)
