Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
उत्तर
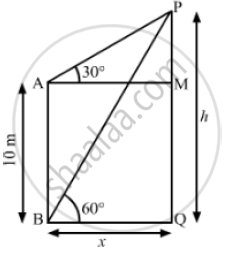
Let PQ be the tower
We have,
AB =10m,MAP = 30° and ∠PBQ = 60°
Also, MQ = AB =10m
Let BQ = x and PQ = h
So, AM = BQ = x and PM = PQ - MQ = h -10
In ΔBPQ,
` tan 60° = (PQ)/(BQ)`
`⇒ sqrt(3) = h/x`
`⇒ x = h/sqrt(3) ` ..............(1)
Now , in Δ AMP
` tan 30° = (PM) /( AM)`
`⇒ 1/ sqrt(3) = (h-10) /x`
`⇒h sqrt(3)-10 sqrt(3)=x`
`⇒ h sqrt(3) - 10 sqrt(3) = h/ sqrt(3) ` [ Using (1)]
⇒ 3h - 30=h
⇒ 3h - h = 30
⇒ 2h = 30
`⇒ h 30/2 `
∴ h = 15 m
So, the height of the tower is 15 m.
संबंधित प्रश्न
A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.
`("Take"sqrt3=1.732)`
A tower stands vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
In given figure, the value of CE is ____________.
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
