Advertisements
Advertisements
Question
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
Solution
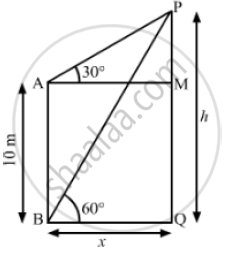
Let PQ be the tower
We have,
AB =10m,MAP = 30° and ∠PBQ = 60°
Also, MQ = AB =10m
Let BQ = x and PQ = h
So, AM = BQ = x and PM = PQ - MQ = h -10
In ΔBPQ,
` tan 60° = (PQ)/(BQ)`
`⇒ sqrt(3) = h/x`
`⇒ x = h/sqrt(3) ` ..............(1)
Now , in Δ AMP
` tan 30° = (PM) /( AM)`
`⇒ 1/ sqrt(3) = (h-10) /x`
`⇒h sqrt(3)-10 sqrt(3)=x`
`⇒ h sqrt(3) - 10 sqrt(3) = h/ sqrt(3) ` [ Using (1)]
⇒ 3h - 30=h
⇒ 3h - h = 30
⇒ 2h = 30
`⇒ h 30/2 `
∴ h = 15 m
So, the height of the tower is 15 m.
RELATED QUESTIONS
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

Two points A and B are on the same side of a tower and in the same straight line with its base. The angles of depression of these points from the top of the tower are 60° and 45° respectively. If the height of the tower is 15 m, then find the distance between the points.
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
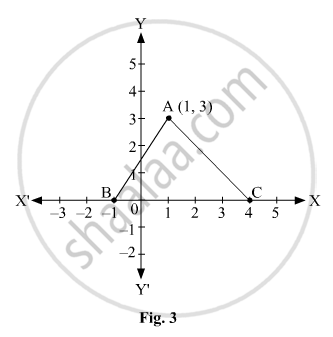
In Fig. 3, the area of triangle ABC (in sq. units) is:
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 600 to the horizontal and reaches upto a point D of pole . If AD = 2.54 m , find the length of the ladder.
The length of the shadow of a tower standing on level ground is found to be 2x metres longer when the sun's elevation is 30°than when it was 45°. The height of the tower in metres is
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
