Advertisements
Advertisements
Question
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 600 to the horizontal and reaches upto a point D of pole . If AD = 2.54 m , find the length of the ladder.
Solution
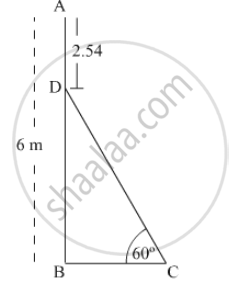
In the given figure,
AB = AD + DB = 6 m
Given: AD = 2.54 m
⇒ 2.54 m + DB = 6 m
⇒ DB = 3.46 m
Now, in the right triangle BCD,
`(BD)/(CD)=sin 60°`
`⇒ (3.46 m)/(CD)=sqrt3/2`
`⇒(3.46 m)/(CD)=1.73/2`
`⇒ CD= (2xx3.46m)/1.73`
`⇒ CD=4 m`
Thus, the length of the ladder CD is 4 m.
APPEARS IN
RELATED QUESTIONS
Two building are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 40 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
The angles of elevation and depression of the top and bottom of a light-house from the top of a 60 m high building are 30° and 60° respectively. Find (i) the difference between the heights of the light-house and the building. (ii) the distance between the light-house and the building.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle elevation of the top of the tower is 60°, What is the height of the tower?
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)

