Advertisements
Advertisements
Question
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff. At a point on the plane 70 metres away from the tower, an observer notices that the angles of elevation of the top and the bottom of the flagstaff are respectively 60° and 45°. Find the height of the flag-staff and that of the tower.
Solution
Let BC be the tower of height x m and AB be the flagstaff of height y, 70 m away from the tower, makes an angle of elevation are 60° and 45° respectively from top and bottom of the flagstaff.
Let AB = y m, BC = x m and CD = 70 m.
So we use trigonometric ratios.
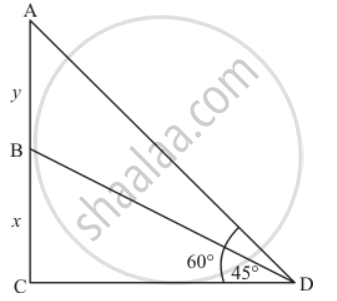
In a triangle BCD
`=> tan D = (BC)/(CD)`
`=> tan 45^@ = x/70`
`=> 1 = 70/x`
`=> x = 70`
Again in a triangle ADC
`=> tan D = (AB + BC)/(CD)`
`=> tan 60^@ = (y + x)/70`
`=> sqrt3 = (y + 70)/70`
`=> 70sqrt3 = 70 + y`
`=> y = 70(sqrt3 - 1)`
=>y = 51.24
Hence the height of flag staff is 51.24 m and height of tower is 70 m
APPEARS IN
RELATED QUESTIONS
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
A storm broke a tree and the treetop rested 20 m from the base of the tree, making an angle of 60° with the horizontal. Find the height of the tree.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
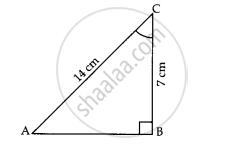
In given figure, the value of ZC is ____________.
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
