Advertisements
Advertisements
Question
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
Options
\[15\sqrt{3}m\]
\[\frac{15\sqrt{3}}{2}m\]
\[\frac{15}{2}\]
15 m
Solution
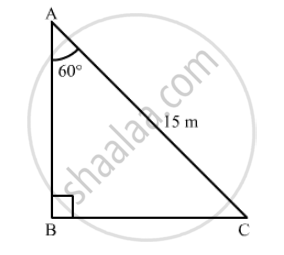
Suppose AB is the wall and AC is the ladder.
It is given that, AC = 15 m and \[\angle\]CAB = 60°.
In right ∆ABC,
\[ \Rightarrow \frac{1}{2} = \frac{AB}{15}\]
\[ \Rightarrow AB = \frac{15}{2} m\]
Thus, the height of the wall is \[\frac{15}{2}\]
APPEARS IN
RELATED QUESTIONS
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
A boat is being rowed away from a cliff 150m high. At the top of the cliff the angle of depression of the boat changes from 60º to 45º in 2 minutes. Find the speed of the boat.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
The angle of elevation of the top of an unfinished tower at a distance of 75m from its base is 30° .How much higher must the tower be raised so that the angle of elevation of its top at the same point may be 60 .
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
A solid right-circular cone of height 60 cm and radius 30 cm is dropped in a right-circular cylinder full of water of height 180 cm and radius 60 cm. Find the volume of water left in the cylinder, in cubic metres ?
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
Water flows at the rate of 10 meters per minute through a cylindrical pipe having its diameter 20 mm. how much time will it take to fill a conical vessel of diameter 40 cm and depth 24 cm?
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
