Advertisements
Advertisements
Question
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
Solution
Let P be the cloud and Q be its reflection.
Let A be the point of observation such that AB = h
Let the height of the cloud be x. ...(PS = x)
PR = x – h and QR = x + h
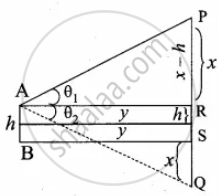
Let AR = y
In the right ∆ARP, tan θ1 = `"PR"/"AR"`
tan θ1 = `(x - "h")/y` ...(1)
In the ∆AQR,
tan θ2 = `"QR"/"AR"`
tan θ2 = `(x + "h")/y` ...(2)
Add (1) and (2)
tan θ1 + tan θ2 = `(x - "h")/y + (x + "h")/y`
= `(x - "h" + x + "h")/y`
= `(2x)/y`
Subtract (2) and (1)
tan θ2 − tan θ1 = `(x + "h")/y - (x - "h")/y`
= `(x + "h" - x + "h")/y`
= `(2"h")/y`
`((tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1) = (2x)/y ÷ (2"h")/y`
= `(2x)/y xx y/(2"h")`
= `x/"h"`
∴ x = `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
Hence the proof.
APPEARS IN
RELATED QUESTIONS
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
|
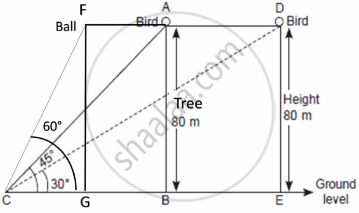
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?