Advertisements
Advertisements
Question
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
Solution
Let AB and CD be the two towers of heights x and y, respectively.
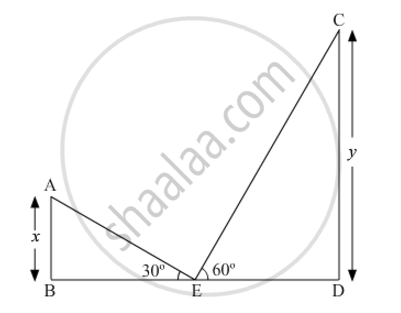
Suppose E is the centre of the line joining the feet of the two towers i.e. BD.
Now, in ∆ABE,
`(AB)/(BE)=tan30^@`
`=>x/(BE)=1/sqrt3`
`=>BE=sqrt3x" ....(1)"`
Also
In ∆CDE,
`(CD)/(DE)=tan60^@`
`=>y/(DE)=sqrt3`
`=>DE=y/sqrt3"....(2)"`
Now, BE = DE .....(3) (E is mid-point of BD.)
So, from (1), (2) and (3), we get
`sqrt3x= y/sqrt3`
`=>x/y=1/3`
Hence, the ratio of x and y is 1 : 3.
APPEARS IN
RELATED QUESTIONS
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
If the elevation of the sun changed from 30º to 60º, then find the difference between the lengths of shadows of a pole 15 m high, made at these two positions
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
The vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height 6m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is
30 and that of the top of the flagstaff 60 . Find the height of the tower
[Use `sqrt(3)` 1.732 ]
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top of the tower from the eye of the observer.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
