Advertisements
Advertisements
Question
A monkey is climbing a rope of length 15 m in a circus. The rope is tied to a vertical pole from its top. Find the height of the pole, if the angle, the rope makes with the ground level is equal to 60°.
Solution
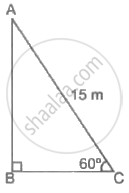
The pole AB in the illustration is where the rope is attached from point C on the ground.
So, AC = 15 m, ∠ACB = 60°
Now, in ΔABC,
`(AB)/(AC)` = sin 60°
`(AB)/15 = sqrt(3)/2`
AB = `(15sqrt(3))/2`
AB = 12.99 m
As a result, the pole's height is 12.99 m.
APPEARS IN
RELATED QUESTIONS
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
The angles of elevation of the top of a rock from the top and foot of a 100 m high tower are respectively 30° and 45°. Find the height of the rock.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
The height of a tower is 10 m. What is the length of its shadow when Sun's altitude is 45°?
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60ϒ and from the same point the angle of elevation of the top of the pedestal is 40ϒ. Find the height of the pedestal. (tan 40° = 0.8391, `sqrt(3)` = 1.732)
A flag pole ‘h’ metres is on the top of the hemispherical dome of radius ‘r’ metres. A man is standing 7 m away from the dome. Seeing the top of the pole at an angle 45° and moving 5 m away from the dome and seeing the bottom of the pole at an angle 30°. Find the height of the pole `(sqrt(3) = 1.732)`

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 2m and is inclined at an angle of 30° to the ground. What should be the length of the slide?
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 meters towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower ____________.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
From the base of a pole of height 20 meter, the angle of elevation of the top of a tower is 60°. The pole subtends an angle 30° at the top of tower. Then the height of tower is ______.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60° and when he retires 40 meters away from the tree the angle of elevation becomes 30°. The breadth of the river is ______.
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 30°. Determine the height of the tower.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
