Advertisements
Advertisements
Question
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
Options
100\[\sqrt{3}\]
\[\frac{100}{\sqrt{3}} m\]
\[50 \sqrt{3}\]
\[\frac{200}{\sqrt{3}} m\]
Solution
Let AB be the height of tower is h meters
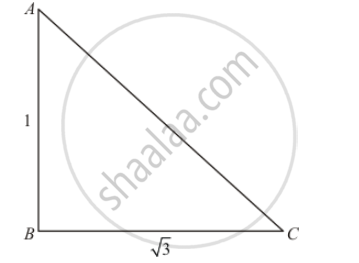
Given that: angle of elevation is `60°` from tower of foot and distance `BC=100` meters.
Here, we have to find the height of tower.
So we use trigonometric ratios.
In a triangle ABC
`⇒ tan C= (AB)/(BC)`
`⇒tan 60°= (AB)/(BC)`
`⇒ sqrt3= h/100`
`⇒ h= 100sqrt3`
APPEARS IN
RELATED QUESTIONS
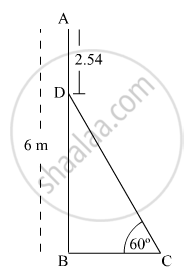
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
Two towers A and B are standing some distance apart. From the top of tower A, the angle of depression of the foot of tower B is found to be 30°. From the top of tower B, the angle of depression of the foot of tower A is found to be 60°. If the height of tower B is ‘h’ m then the height of tower A in terms of ‘h’ is ____________ m.
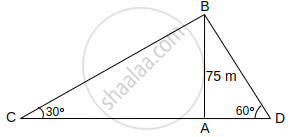
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.