Advertisements
Advertisements
Question
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
Solution
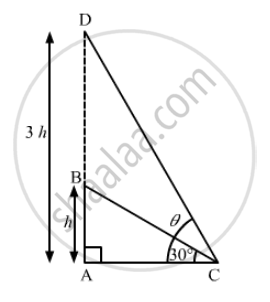
Let the height of the tower AB be h units.
Suppose C is a point on the ground such that ∠ACB=30°
In right ∆ACB,
`tan 30°= (AB)/(AC)`
`⇒ 1/sqrt3=h/(AC)`
`⇒ AC=sqrt3h` ................(1)
Let the angle of elevation of the top of the tower at C be θ, if the height of the tower is tripled.
New height of the tower, AD = 3h units
In right ∆ACD,
`tan θ= (AD)/(AC)`
`⇒ tan θ =(3h)/(AC) `
`⇒ tan θ= (3h)/sqrt(3h)=sqrt3` [from (1)]
`⇒ tan θ= tan 60°`
`⇒ θ=60°`
Hence, the required angle of elevation is 60º.
APPEARS IN
RELATED QUESTIONS
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The angle of elevation of an aeroplane from a point on the ground is 45°. After a flight of 15 seconds, the elevation changes to 30°. If the aeroplane is flying at a height of 3000 metres, find the speed of the aeroplane.
The angle of elevation of a stationary cloud from a point 2500 m above a lake is 15° and the angle of depression of its reflection in the lake is 45°. What is the height of the cloud above the lake level? (Use tan 15° = 0.268)
The horizontal distance between two towers is 60 meters. The angle of depression of the top of the first tower when seen from the top of the second tower is 30° . If the height of the second tower is 90 meters. Find the height of the first tower.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. [Use`pi22/7` ]
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
