Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
उत्तर
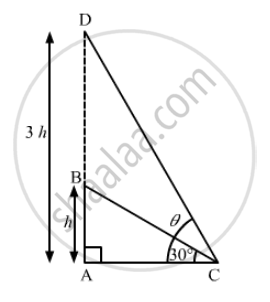
Let the height of the tower AB be h units.
Suppose C is a point on the ground such that ∠ACB=30°
In right ∆ACB,
`tan 30°= (AB)/(AC)`
`⇒ 1/sqrt3=h/(AC)`
`⇒ AC=sqrt3h` ................(1)
Let the angle of elevation of the top of the tower at C be θ, if the height of the tower is tripled.
New height of the tower, AD = 3h units
In right ∆ACD,
`tan θ= (AD)/(AC)`
`⇒ tan θ =(3h)/(AC) `
`⇒ tan θ= (3h)/sqrt(3h)=sqrt3` [from (1)]
`⇒ tan θ= tan 60°`
`⇒ θ=60°`
Hence, the required angle of elevation is 60º.
APPEARS IN
संबंधित प्रश्न
The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
If a man standing on a platform 3 meters above the surface of a lake observes a cloud and its reflection in the lake, then calculate the angle of elevation of the cloud.
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
