Advertisements
Advertisements
प्रश्न
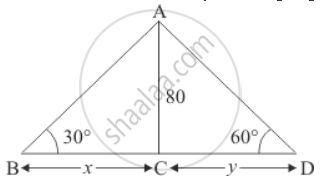
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
उत्तर
Let AB and AD be the two men either side of cliff and height of cliff is 80 m.
And makes an angle of elevation, 30° and 60° respectively of the top of the cliff
We have given that AC = 80 m. Let BC = x and CD = y. And ∠ABC = 30°, ∠ADC = 60°
Here we have to find height of cliff.
So we use trigonometric ratios
In a triangle ABC
`=> tan B = (AC)/(BC)`
`=> tan 30^@ = 80/x`
`=> 1/sqrt3 = 80/x`
`=> x = 80sqrt3`
Again in a triangle ADC
`=> tan D = (AC)/(CD)`
`=> tan 60^@ = 80/y`
`=> sqrt3 = 80/y`
`=> y = 80/sqrt3`
`=> x + y = 80sqrt3 + 80/sqrt3`
`=> x + y = 320/sqrt3`
=> x + y = 184.8
Hence the height of cliff is 184.8 m
APPEARS IN
संबंधित प्रश्न
A bucket open at the top is in the form of a frustum of a cone with a capacity of 12308.8 cm3. The radii of the top and bottom circular ends are 20 cm and 12 cm, respectively. Find the height of the bucket and the area of metal sheet used in making the bucket. (use π = 3.14)
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30°. Find the distance travelled by the balloon during the interval.

A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
The angles of depression of two ships from the top of a lighthouse and on the same side of it are found to be 45° and 30° respectively. If the ships are 200 m apart, find the height of the lighthouse.
On a horizonal plane there is a vertical tower with a flagpole on the top of the tower. At a point, 9 meters away from the foot of the tower, the angle of elevation of the top and bottom of the flagpole are 60 and 30 respectively. Find the height of the tower and the flagpole mounted on it.
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
