Question

From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is

पर्याय

• \[\left( \sqrt{3} + 1 \right) \text{ h metres }\]

• \[\left( \sqrt{3} - 1 \right) \text{ h metres }\]

• \[\sqrt{3} \text{ h metres }\]

• \[1 + \left( 1 + \frac{1}{\sqrt{3}} \right) \text{ h metres }\]

Answer 1

Let the height of the light house AB be h meters

Given that: angle of depression of ship are`∠C=30`  and`∠D=45°`

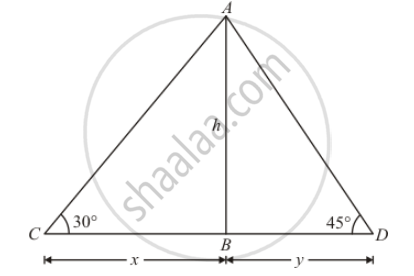
Distance of the ship C =`BC=x`  and distance of the ship D =`BD=y`

Here, we have to find distance between the ships.

So we use trigonometric ratios.

In a triangle,`ABC`

`⇒ tan C=(AB)/(BC)`  

`⇒ tan 30°=h/x` 

`⇒1/sqrt3=h/x`

`⇒ x=sqrt(3h)` 

Again in a triangle ABD, 

`tan D=(AB)/(BD)` 

`⇒ tan D= (AB)/(BD)`

`⇒ tan 45°=h/y`

`⇒ 1=h/y`

`⇒ y=h`

Now, distance between the ships `=x+y=sqrt3h+h(sqrt3+1)h`