Advertisements
Advertisements
प्रश्न
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
विकल्प
\[\left( \sqrt{3} + 1 \right) \text{ h metres }\]
\[\left( \sqrt{3} - 1 \right) \text{ h metres }\]
\[\sqrt{3} \text{ h metres }\]
\[1 + \left( 1 + \frac{1}{\sqrt{3}} \right) \text{ h metres }\]
उत्तर
Let the height of the light house AB be h meters
Given that: angle of depression of ship are`∠C=30` and`∠D=45°`
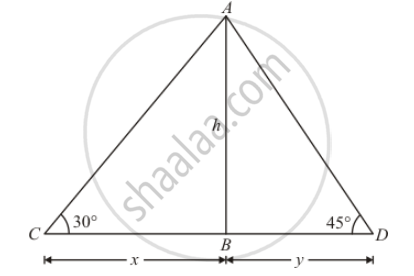
Distance of the ship C =`BC=x` and distance of the ship D =`BD=y`
Here, we have to find distance between the ships.
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=(AB)/(BC)`
`⇒ tan 30°=h/x`
`⇒1/sqrt3=h/x`
`⇒ x=sqrt(3h)`
Again in a triangle ABD,
`tan D=(AB)/(BD)`
`⇒ tan D= (AB)/(BD)`
`⇒ tan 45°=h/y`
`⇒ 1=h/y`
`⇒ y=h`
Now, distance between the ships `=x+y=sqrt3h+h(sqrt3+1)h`
APPEARS IN
संबंधित प्रश्न
A man on a cliff observes a fishing trawler at an angle of depression of 30º which is approaching the shore to the point immediately beneath the observer with a uniform speed. 6 minutes later, the angle of depression of the trawler is found to be 60º. Caliculate the time taken by the trawler to reach the shore
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use `sqrt3` = 1⋅732]
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30º. The distance of the car from the tower (in metres) is
A window of a house is h metres above the ground. From the window, the angles of elevation and depression of the top and the bottom of another house situated on the opposite side of the lane are found to be α and β, respectively. Prove that the height of the other house is h(1+ tan α tan β) metres.
