Advertisements
Advertisements
प्रश्न
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
उत्तर
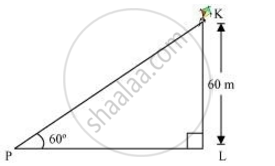
Let K be the kite and the string is tied to point P on the ground.
In ΔKLP,
`("KL")/("KP") = sin 60°`
`60/("KP") = sqrt3/2`
KP = `120/sqrt3`
KP = `40sqrt3` m
Hence, the length of the string is `40sqrt3` m.
APPEARS IN
संबंधित प्रश्न
A person standing on the bank of river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. `(sqrt 3=1.73)`
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships
The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
A balloon is connected to a meteorological ground station by a cable of length 215 m inclined at 600 to the horizontal. Determine the height of the balloon from the ground. Assume that there is no slack in the cable.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
From the top of the tower h metre high , the angles of depression of two objects , which are in the line with the foot of the tower are ∝ and ß (ß> ∝ ) cts .
The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower the angle of elevation is found to be β. The height of the tower is
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is `30sqrt(3)` feet from the entrance of the lift, find the speed of the lift which is descending.
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
The distance of point A(-5, 6) from the origin is ______.
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
A statue, 2 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
In the given figure, AB is tower of height 50 m. A man standing on its top, observes two car on the opposite sides of the tower with angles of depression 30° and 45° respectively. Find the distance between the two cars.

The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
