Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
उत्तर
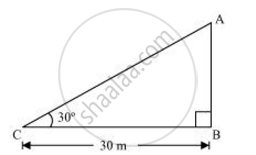
Let AB be the tower and the angle of elevation from point C (on ground) is 30°.
In ΔABC,
`("AB")/("BC") = tan 30°`
`("AB")/(30) = 1/sqrt3`
AB = `(30)/sqrt3`
AB = `(30)/sqrt3 xxsqrt3/sqrt3`
AB = `10sqrt3` m
Therefore, the height of the tower is `10sqrt3` m.
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
A balloon of radius γ makes an angle α at the eye of an observer and the angle of elevation of its centre is β. Then find the height of its centre from the ground level
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
From the top of a tower, 100, high, a man observes two cars on the opposite sides of the tower and in same straight line with its base, with angles of depression 30° and 45°. Find the distance between the cars. [Take `sqrt3` = 1.732]
A kit is flying at a height of 75 metres from the ground level, attached to a string inclined at 60 to the horizontal. Find the length of the string to the nearest metre.
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
From the top of a lighthouse, an observer looking at a ship makes angle of depression of 60°. If the height of the lighthouse is 90 metre, then find how far the ship is from the lighthouse.
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
In given figure, the value of AE is ____________.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
