Advertisements
Advertisements
प्रश्न
The length of shadow of a tower on the plane ground is `sqrt3` times the height of the tower.
The angle of elevation of sun is:
विकल्प
A. 45°
B. 30°
C. 60°
D. 90°
उत्तर
Let AB be the tower and BC be the length of the shadow of the tower.
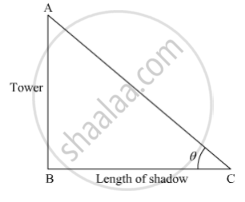
Here, θ is the angle of elevation of the sun.
Given, length of shadow of tower = `sqrt3` × Height of the tower
BC = `sqrt3` AB ... (1)
In right ΔABC
`tanO/=(AB)/(BC)` `(tanO/=(\text{opposite side})/\text{opposite side})`
`thereforetanO/=(AB)/sqrt(AB)` `\text{Using} (1)`
`rArrtanO/=1/sqrt3`
`rArrtan=tan 30^@` `(thereforetan30^@=1/sqrt3)`
`rArrO/=30^@`
Thus, the angle of elevation of the sun is 30°.
Hence, the correct answer is B.
संबंधित प्रश्न
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
If the angle of elevation of cloud from a point 200 m above a lake is 30º and the angle of depression of its reflection in the lake is 60º, then find the height of the cloud above the lake
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
If sin θ = cos θ , then 2 tan2θ + sin2θ – 1 is equal to
The angle of elevation of a cloud from a point h metres above a lake is β. The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is
If one looks from a tower 10 m high at the top of a flag staff, the depression angle of 30° is made. Also, looking at the bottom of the staff from the tower, the angle of the depression made is of 60°. Find the height of the flag staff.
Read the following passage:
A boy is standing on the top of light house. He observed that boat P and boat Q are approaching the light house from opposite directions. He finds that angle of depression of boat P is 45° and angle of depression of boat Q is 30°. He also knows that height of the light house is 100 m.
|
Based on the above information, answer the following questions.
- What is the measure of ∠APD?
- If ∠YAQ = 30°, then ∠AQD is also 30°, Why?
- Find length of PD
OR
Find length of DQ


