Question

The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]

Answer 1

Let h be the height of the tower and the angle of elevation as observed from the foot of the tower is 32° and observed move towards the tower with distance 100 m then the angle of elevation becomes 63°.

Let BC = x and CD = 100

Now we have to find the height of the tower

So we use trigonometrical ratios.

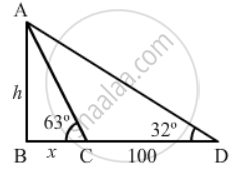
In a triangle ABC,

`=> tan C = (AB)/(BC)`

`=> tan 63^@ = (AB)/(BC)`

`=> 1.9626 = h/x`

`=> x = h/1.9626`

Again in a triangle ABD

`=> tan D = (AB)/(BC + CD)`

`=> tan 32^@ = h/(x + 100)`

`=> 0.6248 = h/(x + 100)`

`=> x + 100 = h/0.6248`

`=> 100 = h/0.6248 - h/1.9626` 

`=> 100 = (h xx 1.9626 - h xx 0.6248)/(0.6248 xx 1.9626)`

`=> 100 = (h(1.9626 - 0.6248))/(0.6248 xx 1.9626)`

`=> 100 = (h(1.3378))/(0.6248 xx 1.9626)`

=> 100 x 0.6248 x 1.9626 = h x 1.3378

`=> h = (100 xx 0.6248 xx 1.9626)/1.3378`

`=> 122.6232/1.3378`

=> 91.66

`=> x = 91.66/1.9626`

= 46.7

So distance of the first position from the tower is = 100 + 46.7 = 146.7 m

Hence the height of tower 91.66 m and the desires distance is  146.7 m