Advertisements
Advertisements
प्रश्न
The angle of elevation of a tower from a point on the same level as the foot of the tower is 30°. On advancing 150 metres towards the foot of the tower, the angle of elevation of the tower becomes 60°. Show that the height of the tower is 129.9 metres (Use `sqrt3 = 1.732`)
उत्तर
Let h be the height of tower and angle of elevation of the foot of the tower is 30°, on advancing 150 m towards the foot of tower then an angle of elevation becomes 60°.
We assume that BC = x and CD = 150 m.
Now we have to prove height of the tower is 129.9 m.
So we use trigonometrical ratios.
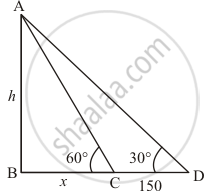
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 60^@ = (AB)/(BC)`
`=> sqrt3 = h/x`
`=> h/sqrt3 = x`
Again in a triangle ABD
`=> tan D = (AB)/(BC + CD)`
`=> tan 30^@ = h/(x + 150)`
`=> 1/sqrt3 = h/(x + 150)`
`=> x + 150 = sqrt3h`
`=> x = sqrt3h - 150`
`=> h/sqrt3 = sqrt3 - 150`
`=> h = 3h - 150sqrt3`
`=> 2h = 150sqrt3`
`=> h = (150 xx 1.732)/2`
=> h = 129.9
Hence the height of tower is 129.9 m proved
APPEARS IN
संबंधित प्रश्न
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
The angle of elevation of the top of a tower as observed form a point in a horizontal plane through the foot of the tower is 32°. When the observer moves towards the tower a distance of 100 m, he finds the angle of elevation of the top to be 63°. Find the height of the tower and the distance of the first position from the tower. [Take tan 32° = 0.6248 and tan 63° = 1.9626]
Two ships are approaching a light-house from opposite directions. The angles of depression of the two ships from the top of the light-house are 30° and 45°. If the distance between the two ships is 100 m, find the height of the light-house. \[[Use \sqrt{3} = 1 . 732]\]
If the ratio of the height of a tower and the length of its shadow is `sqrt3:1`, what is the angle of elevation of the Sun?
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.
From the top of an 8 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower. (Take `sqrt(3)` = 1.732).
The top of a hill when observed from the top and bottom of a building of height h is at angles of elevation p and q respectively. What is the height of the hill?
